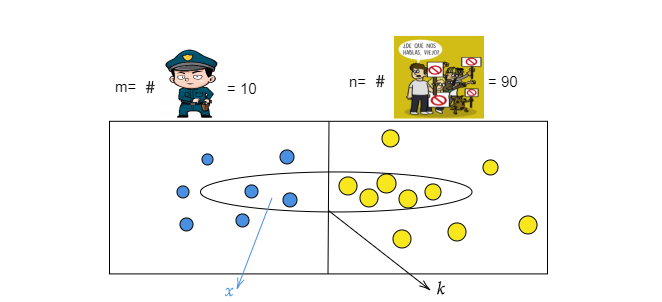
Algunas veces podríamos tener situaciones donde de una población se debe extraer una muestra sin reemplazo. Este tipo de experimento será llamado experimento hipergeométrico.
- De un lote de \(N=m+n\) artículos se selecciona una muestra aleatoria de tamaño \(k\) sin reemplazo
- \(m\) de los \(N=m+n\) artículos se pueden clasificar como éxitos y \(n\) como fracasos
el número \(X\) de éxitos de un experimento hipergeométrico se denomina variable aleatoria hipergeométrica.