An Introduction to Bayesian Inference
Rose Maier & Jacob Levernier
PSY612, Winter 2015
Probability
The frequentist framework is concerned with the frequency of hypothetical events.
- Your data are assumed to be one possible sample from an infinite set of possible samples, and your result is compared to the rest of that hypothetical sampling distribution to estimate its probability.
- Your parameter estimates are generally assumed to be fixed - there is some true, exact underlying population value.
Probability theory is directly concerned with the probability of events.
- Your data are assumed to be fixed, there is no hypothetical sampling distribution.
- Your parameters are assumed to be random - they come from a probability distribution of parameter estimates.
P(X) = “The probability of X”
Probability Examples
Probabilities are often derived from rates.
For example:
The CDC estimates that 1 in 68 children has been identified with ASD.
P(having ASD) = 1/68 = 0.015
Of the 25 people in PSY612 (students and instructors), 7 have first names that start with the letter “J”.
P(first name starts with J) = 7/25 = 0.28
Conditional Probability
P(X|Y) = “The probability of X, given Y”
- Consider P(a randomly selected child has autism) vs. P(the child has autism | he's male)
- 1 in 68 children has ASD:
P(ASD) = 1/68 = .015 - 1 in 42 boys has ASD:
P(ASD | male) = 1/42 = .024
- 1 in 68 children has ASD:
- P(Y|X) = P(Y&X)/P(X)
- (Notation for this: “and”: ∩ ; “or”: ∪)
A conditional probability is NOT the same as its inverse
ASD and gender
- 1 out of 42 boys has ASD:
- P(ASD|male) = 1/42 = .024
- P(ASD|male) = 1/42 = .024
- A little more than 4 out of 5 children with ASD are male (4.3:1 male to female ratio)
- P(male|ASD) = 4.3/5.3 = .811
- P(male|ASD) = 4.3/5.3 = .811
Names starting with J and GTFs
- 2 out of 3 GTFs have names that start with “J”
- P(J|GTF) = 2/3 = .667
- P(J|GTF) = 2/3 = .667
- 7 people in 612 have names that start with “J” and 2 of them are GTFs
- P(GTF|J) = 2/7 = .286
Conditional Probability and *p* = .05
A p-value = The probability of observing these data (or more extreme), given that the null hypothesis is true
- P(D) = the probability of observing these data or more extreme data
- P(N) = the probability that the null hypothesis is true
- p = P(D|N)
- But what you probably want to know is not whether these data are likely given that the null is true…
- …but, rather, whether the null hypothesis is true or not given these data you've observed: P(N|D)
Bayes' theorem, and its notation
Bayes' Theorem is the equation that describes how a conditional probability is related to its inverse:
P(A|B) = P(B|A)*P(A) / P(B)- More generally,
P(θ|D) = P(D|θ)*P(θ) / P(D)- “posterior = likelihood * prior / evidence”
- P(B) = P(B|A)P(A) + P(B|Not A)P(Not A)
Examples:
- P(ASD|male) =
P(male|ASD) x P(ASD) / P(male) = (.811) x (.015) / (.50) = .024 - P(male|ASD) =
P(ASD|male) x P(male) / P(ASD) = (.024) x (.50) / (.015) = .8
Problems with NHST
The (muddled) logic of p values
- p = P(D|N)
- ? = P(N|D)
This was highlighted in a popular Nature article last year:
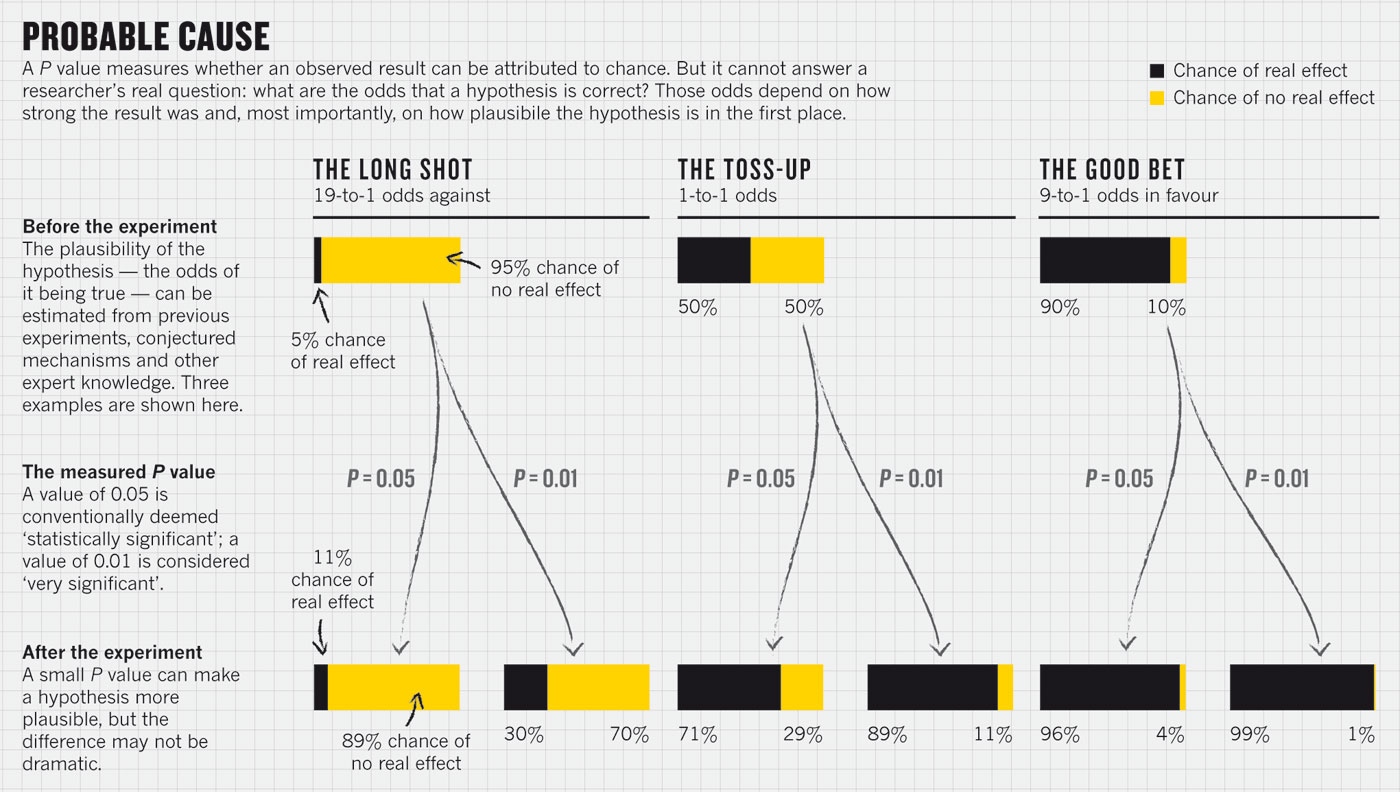
Problems with NHST, cont.
Multiple comparisons
- 30 people into 1 control group, 4 treatment groups (6 people per group). Control vs. T1 yields t = 2.95.
Q: Is that significant?
- RA #1: You give her the two groups. She compares the two groups. Significant!
- RA #2: You give him all five groups, and ask for all pairwise comparisons. Correcting for familywise error, critical t is 3.43. Not significant!
- PI: Intends to do all pairwise comparisons, but asked the first RA to just do the single comparison. Claims significance, but is planning to do multiple comparisons while using a critical t value meant for a single comparison.
Bayes doesn't care about your intentions
- The problem with multiple comparisons in NHST arises when you try to convert a measurement of your data (the test statistic) into a probability (the p value). The mechanics of this conversion rely on a host of assumptions that may or may not be reasonable.
- Bayesian inference skips the issue completely by never having to convert to and from probability estimates.
Clarification: Bayes vs. Frequentist
| Bayesian | Frequentist | |
|---|---|---|
| Estimation | HDIs, ROPEs, posteriors |
CIs, equivalence tests |
| Hypothesis Testing |
BFs | NHST |
Clarification: Bayes vs. Frequentist
Some ideas to keep in mind…
- Estimation approaches in general mean no uninformative results. Hooray!
- Bayesian approaches use estimation more often, frequentist traditionally use mostly hypothesis testing (p values) - but that's about how each tool gets used, not what it's capable of.
- You spell out your model assumptions explicitly with Bayes (although this may become less obvious as the tools become more user-friendly).
Bringing in background knowledge
- “Updating” a prior in future research.
- When you do Bayesian analyses, you explicitly state your prior (i.e., your background assumptions, or lack thereof) to communicate your model.
- What might inform your prior:
- Previous research
- Theory-based assumption
- (Sometimes, you don't have a well-informed prior, so you use something vague.)
We can use *Distributions* of priors!
We can use *Distributions* of priors!
Nuts and bolts
Example time!
Krushke's simple linear regression example: What is the relationship between height and weight?
Nuts and bolts
The prior!
Nuts and bolts
The data!
Nuts and bolts
The posterior!
Nuts and bolts
compare to NHST correlation
Pearson's product-moment correlation
data: x and y
t = 4.4191, df = 28, p-value = 0.0001354
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.3650241 0.8134220
sample estimates:
cor
0.6409977
Nuts and bolts
Nuance in the results
Problems Bayes won't fix for you
- You still need to design a good experiment.
- You still need to worry about random selection and generalizability of your results.
- You still need a good amout of data; the more data you have, the more informative your results will be.
- You still need to worry about experimenter degrees of freedom (although you can relax about multiple comparisons). See this blog post.
How to learn more
- Get a good book (Kruschke, Gelman, L&W, etc.).
- Come to Bayes Club.
- Consider doing a summer workshop. Rose recommends the 4-week Bayes Intro at ICPSR.
- Pester the department Powers That Be to provide us with opportunities to learn this stuff
- Ulrich (head), Sara (GEC), Azim (chair of colloquium committee)
- The quant profs: Lou, Robert, and Elliot (611/612/613), Sanjay (SEM), Gerard (psychometrics)
- MethLab is a great venue for pestering (Sanjay, Elliot, and Rose)
- Let Sara know you'd like to have a Bayesian expert come talk to us for the big data series!
- Ulrich (head), Sara (GEC), Azim (chair of colloquium committee)
Questions?
Bayesian inference elegantly incorporates background knowledge
Bayes Theorem revisited
- P(θ|D) = P(D|θ)*P(θ) / P(D)
- “posterior = likelihood * prior / evidence”
Silver 9-11 example:
Bringing in background knowledge