Alencar Xavier

• Quantitative Geneticist, Corteva Agrisciences
• Adjunct professor, Purdue University
• http://alenxav.wixsite.com/home/

Gota Morota

• Assistent professor, Virginia Tech
• http://morotalab.org/

Part 1: Concepts

• History of mixed models
• Mixed models in plant breeding
• Fixed and random terms
• Model notation
• Variance decomposition

Part 2: Applications

• Selection models
• Practical examples
• Variance components
• Ridges and Kernels

Francis Galton - 1886: Regression and heritability

Ronald Fisher - 1918: Infinitesimal model (P = G + E)

Sewall Wright - 1922: Genetic relationship

Charles Henderson - 1950, 1968: BLUP using relationship

• Heart and soul of plant breeding (Xavier et al 2017)
• Variance components and heritability
• Trait associations (Gianola and Sorensen 2014)
• Estimation of genetic values (Piepho et al 2008)
• Estimation of breeding values
• Prediction of unphenotyped lines (de los Campos et al 2013)
• Selection index
• Genome-wide association analysis (Yang et al 2014)
• All sorts of inference (Robinson 1991)

Fixed effect

• Assumed to be invariable (often you cannot recollect the data)
• Inferences are made upon the parameters
• Results can not be extrapolated to other datasets
• Example: Overall mean and environmental effects

Random effects

• You may not have all the levels available
• Inference are made on variance components
• Prior assumption: coefficients are normally distributed
• Results can not be extrapolated to other datasets
• Example: Genetic effects

• Linear model: \(y=Xb+Zu+e\)
• With variance: \(y \sim N(Xb,ZKZ\sigma^{2}_{u}+I\sigma^{2}_{e})\)

Assuming: \(u \sim N(0,K\sigma^{2}_{u})\) and \(e \sim N(0,I\sigma^{2}_{e})\)

Henderson equation

\[ \left[\begin{array}{rr} X'X & Z'X \\ X'Z & Z'Z+\lambda K^{-1} \end{array}\right] \left[\begin{array}{r} b \\ u \end{array}\right] =\left[\begin{array}{r} X'y \\ Z'y \end{array}\right] \] Summary:

• We know (data): \(x=\{y,X,Z,K\}\)
• We want (parameters): \(\theta=\{b,u,\sigma^{2}_{a},\sigma^{2}_{e}\}\)
• Estimation based on Gaussian likelihood: \(L(x|\theta)\)

• y = vector of observations (n)
• X = design matrix of fixed effects (n x p)
• Z = design (or incidence) matrix of random effects (n x p)
• K = random effect correlation matrix (q x q)
• u = vector of random effect coefficients (q)
• b = vector of fixed effect coefficients (p)
• e = vector of residuals (n)
• \(\sigma^{2}_{a}\) = marker effect variance (1)
• \(\sigma^{2}_{u}\) = random effect variance (1)
• \(\sigma^{2}_{e}\) = residual variance (1)
• \(\lambda=\sigma^{2}_{e}/\sigma^{2}_{u}\) (Regularization parameters) (1)

The mixed model can also be notated as follows

\[y=Wg+e\]

Solved as

\[[W'W+\Sigma] g = [W'y]\]

Where

\(W=[X,Z]\)

\(g=[b,u]\)

\(\Sigma = \left[\begin{array}{rr} 0 & 0 \\ 0 & \lambda K^{-1} \end{array}\right]\)

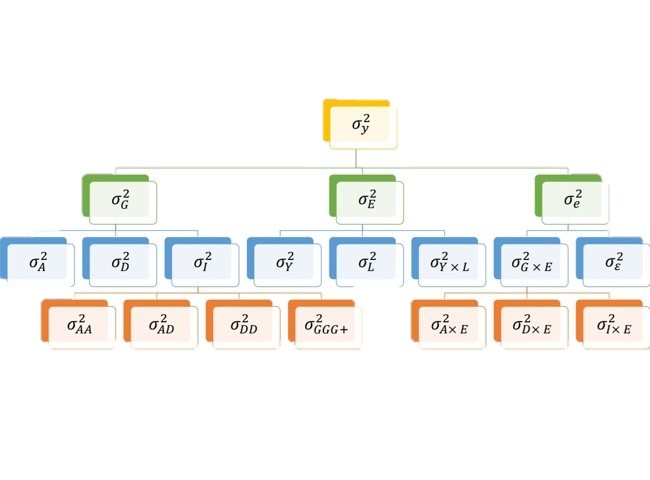
1 Genetic values

• BLUPs or BLUEs from replicated trials
• Captures additive and non-additive genetics together

2 Breeding values

• Use pedigree information to create \(K\)
• Captures additive genetics (heritable)
• Trials not necessarily replicated

3 Genomic Breeding values

• Genotypic information replaces pedigree
• Any signal: additivity, dominance and epistasis

• Example 1: Balanced data, no kinship
• Example 2: Balanced data, with kinship
• Example 3: Unbalanced data, with kinship
• Example 4: Balanced data, missing individual

Data:

##    Env Gen Phe
## 1   E1  G1  47
## 2   E1  G2  51
## 3   E1  G3  46
## 4   E1  G4  58
## 5   E2  G1  52
## 6   E2  G2  46
## 7   E2  G3  52
## 8   E2  G4  54
## 9   E3  G1  53
## 10  E3  G2  48
## 11  E3  G3  58
## 12  E3  G4  52

Model: \(Phenotype = Environment_{(F)} + Genotype_{(R)}\)

Design matrix \(W\):

##    EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## 1      1     0     0     1     0     0     0
## 2      1     0     0     0     1     0     0
## 3      1     0     0     0     0     1     0
## 4      1     0     0     0     0     0     1
## 5      0     1     0     1     0     0     0
## 6      0     1     0     0     1     0     0
## 7      0     1     0     0     0     1     0
## 8      0     1     0     0     0     0     1
## 9      0     0     1     1     0     0     0
## 10     0     0     1     0     1     0     0
## 11     0     0     1     0     0     1     0
## 12     0     0     1     0     0     0     1

\(W'W\):

##       EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## EnvE1     4     0     0     1     1     1     1
## EnvE2     0     4     0     1     1     1     1
## EnvE3     0     0     4     1     1     1     1
## GenG1     1     1     1     3     0     0     0
## GenG2     1     1     1     0     3     0     0
## GenG3     1     1     1     0     0     3     0
## GenG4     1     1     1     0     0     0     3

Left-hand side (\(W'W+\Sigma\)):

##       EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## EnvE1     4     0     0  1.00  1.00  1.00  1.00
## EnvE2     0     4     0  1.00  1.00  1.00  1.00
## EnvE3     0     0     4  1.00  1.00  1.00  1.00
## GenG1     1     1     1  3.17  0.00  0.00  0.00
## GenG2     1     1     1  0.00  3.17  0.00  0.00
## GenG3     1     1     1  0.00  0.00  3.17  0.00
## GenG4     1     1     1  0.00  0.00  0.00  3.17

Assuming independent individuals: \(K=I\)

Regularization: \(\lambda=\sigma^{2}_{e}/\sigma^{2}_{u}=1.64/9.56=0.17\)

Right-hand side (\(W'y\)):

##       [,1]
## EnvE1  202
## EnvE2  204
## EnvE3  211
## GenG1  152
## GenG2  145
## GenG3  156
## GenG4  164

We can find coefficients through least-square solution

\(g=(LHS)^{-1}(RHS)=(W'W+\Sigma)^{-1}W'y\)

##        [,1]
## EnvE1 50.50
## EnvE2 51.00
## EnvE3 52.75
## GenG1 -0.71
## GenG2 -2.92
## GenG3  0.55
## GenG4  3.08

\(BLUE=\frac{w'y}{w'w}=\frac{sum}{n}\) = simple average

\(BLUP=\frac{w'y}{w'w+\lambda}=\frac{sum}{n+\lambda}\) = biased average = \(BLUE\times h^2\)

Note:

• More observations = less shrinkage
• Higher heritability = less shrinkage: \(\lambda = \frac{h^{2}-1}{h^2}\)

If we know the relationship among individuals:

##       GenG1 GenG2 GenG3 GenG4
## GenG1  1.00  0.64  0.23  0.48
## GenG2  0.64  1.00  0.33  0.67
## GenG3  0.23  0.33  1.00  0.31
## GenG4  0.48  0.67  0.31  1.00

Then we estimate \(\lambda K^{-1}\)

##       GenG1 GenG2 GenG3 GenG4
## GenG1  0.15 -0.09  0.00 -0.01
## GenG2 -0.09  0.22 -0.02 -0.10
## GenG3  0.00 -0.02  0.10 -0.02
## GenG4 -0.01 -0.10 -0.02  0.17

Regularization: \(\lambda=\sigma^{2}_{e}/\sigma^{2}_{u}=1.64/17.70=0.09\)

And the left-hand side becomes

##       EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## EnvE1     4     0     0  1.00  1.00  1.00  1.00
## EnvE2     0     4     0  1.00  1.00  1.00  1.00
## EnvE3     0     0     4  1.00  1.00  1.00  1.00
## GenG1     1     1     1  3.15 -0.09  0.00 -0.01
## GenG2     1     1     1 -0.09  3.22 -0.02 -0.10
## GenG3     1     1     1  0.00 -0.02  3.10 -0.02
## GenG4     1     1     1 -0.01 -0.10 -0.02  3.17

We can find coefficients through least-square solution

\(g=(LHS)^{-1}(RHS)=(W'W+\Sigma)^{-1}W'y\)

##        [,1]
## EnvE1 51.05
## EnvE2 51.55
## EnvE3 53.30
## GenG1 -1.32
## GenG2 -3.34
## GenG3  0.03
## GenG4  2.45

Genetic coefficients shrink more: Var(A) < Var(G)

What if we have missing data?

##    Env Gen Phe
## 1   E1  G1  47
## 2   E1  G2  51
## 3   E1  G3  NA
## 4   E1  G4  58
## 5   E2  G1  52
## 6   E2  G2  46
## 7   E2  G3  52
## 8   E2  G4  NA
## 9   E3  G1  53
## 10  E3  G2  48
## 11  E3  G3  58
## 12  E3  G4  52

Rows of missing points are removed

##    EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## 1      1     0     0     1     0     0     0
## 2      1     0     0     0     1     0     0
## 4      1     0     0     0     0     0     1
## 5      0     1     0     1     0     0     0
## 6      0     1     0     0     1     0     0
## 7      0     1     0     0     0     1     0
## 9      0     0     1     1     0     0     0
## 10     0     0     1     0     1     0     0
## 11     0     0     1     0     0     1     0
## 12     0     0     1     0     0     0     1

\(W'W\):

##       EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## EnvE1     3     0     0     1     1     0     1
## EnvE2     0     3     0     1     1     1     0
## EnvE3     0     0     4     1     1     1     1
## GenG1     1     1     1     3     0     0     0
## GenG2     1     1     1     0     3     0     0
## GenG3     0     1     1     0     0     2     0
## GenG4     1     0     1     0     0     0     2

Left-hand side (\(W'W+\Sigma\)):

##       EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## EnvE1     3     0     0  1.00  1.00  0.00  1.00
## EnvE2     0     3     0  1.00  1.00  1.00  0.00
## EnvE3     0     0     4  1.00  1.00  1.00  1.00
## GenG1     1     1     1  3.10 -0.06  0.00 -0.01
## GenG2     1     1     1 -0.06  3.15 -0.01 -0.07
## GenG3     0     1     1  0.00 -0.01  2.07 -0.01
## GenG4     1     0     1 -0.01 -0.07 -0.01  2.11

Regularization: \(\lambda=\sigma^{2}_{e}/\sigma^{2}_{u}=1.21/19.61=0.06\)

Right-hand side (\(W'y\)):

##       [,1]
## EnvE1  156
## EnvE2  150
## EnvE3  211
## GenG1  152
## GenG2  145
## GenG3  110
## GenG4  110

Find coefficients through least-square solution

\(g=(LHS)^{-1}(RHS)=(W'W+\Sigma)^{-1}W'y\)

##        [,1]
## EnvE1 54.14
## EnvE2 51.70
## EnvE3 53.82
## GenG1 -2.56
## GenG2 -4.68
## GenG3  2.15
## GenG4  0.81

What if we are missing data from a individual?

##    Env Gen Phe
## 1   E1  G1  NA
## 2   E1  G2  51
## 3   E1  G3  46
## 4   E1  G4  58
## 5   E2  G1  NA
## 6   E2  G2  46
## 7   E2  G3  52
## 8   E2  G4  54
## 9   E3  G1  NA
## 10  E3  G2  48
## 11  E3  G3  58
## 12  E3  G4  52

Rows of missing points are removed

##    EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## 2      1     0     0     0     1     0     0
## 3      1     0     0     0     0     1     0
## 4      1     0     0     0     0     0     1
## 6      0     1     0     0     1     0     0
## 7      0     1     0     0     0     1     0
## 8      0     1     0     0     0     0     1
## 10     0     0     1     0     1     0     0
## 11     0     0     1     0     0     1     0
## 12     0     0     1     0     0     0     1

\(W'W\):

##       EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## EnvE1     3     0     0     0     1     1     1
## EnvE2     0     3     0     0     1     1     1
## EnvE3     0     0     3     0     1     1     1
## GenG1     0     0     0     0     0     0     0
## GenG2     1     1     1     0     3     0     0
## GenG3     1     1     1     0     0     3     0
## GenG4     1     1     1     0     0     0     3

Left-hand side (\(W'W+\Sigma\)):

##       EnvE1 EnvE2 EnvE3 GenG1 GenG2 GenG3 GenG4
## EnvE1     3     0     0  0.00  1.00  1.00  1.00
## EnvE2     0     3     0  0.00  1.00  1.00  1.00
## EnvE3     0     0     3  0.00  1.00  1.00  1.00
## GenG1     0     0     0  0.14 -0.08  0.00 -0.01
## GenG2     1     1     1 -0.08  3.19 -0.02 -0.09
## GenG3     1     1     1  0.00 -0.02  3.09 -0.01
## GenG4     1     1     1 -0.01 -0.09 -0.01  3.15

Regularization: \(\lambda=\sigma^{2}_{e}/\sigma^{2}_{u}=1.79/22.78=0.08\)

Right-hand side (\(W'y\)):

##       [,1]
## EnvE1  155
## EnvE2  152
## EnvE3  158
## GenG1    0
## GenG2  145
## GenG3  156
## GenG4  164

Find coefficients through least-square solution

\(g=(LHS)^{-1}(RHS)=(W'W+\Sigma)^{-1}W'y\)

##        [,1]
## EnvE1 52.06
## EnvE2 51.06
## EnvE3 53.06
## GenG1 -1.82
## GenG2 -3.48
## GenG3 -0.07
## GenG4  2.38

Expectation-Maximization REML (1977)

\(\sigma^{2}_{u} = \frac{u'K^{-1}u}{q-\lambda tr(K^{-1}C^{22})}\) and \(\sigma^{2}_{e} = \frac{e'y}{n-p}\)

Bayesian Gibbs Sampling (1993)

\(\sigma^{2}_{u} = \frac{u'K^{-1}u+S_u\nu_u}{\chi^2(q+\nu_u)}\) and \(\sigma^{2}_{e} = \frac{e'e+S_e\nu_e}{\chi^2(n+\nu_e)}\)

Predicted Residual Error Sum of Squares (PRESS) (2017)

• \(\lambda = argmin(\sum{e^2_i/(1-h_{ii})^2})\)
• Where \(H=(I+K\lambda)^{-1}\) and \(e=y-\mu-Hy\)

Kernel methods:

• Genetic signal is captured by the relationship matrix \(K\)
• Random effect coefficients are the breeding values (BV)
• Efficient to compute BV when \(markers \gg individuals\)
• Easy use and combine pedigree, markers and interactions

Ridge methods:

• Genetic signal is captured by the design matrix \(M\)
• Random effect coefficients are the marker effects
• Easy way to make predictions of unobserved individuals
• Enables to visualize where the QTLs are in the genome

Kernel

\(y=Xb+Zu+e\), \(u\sim N(0,K\sigma^2_u)\)

Ridge

\(y=Xb+Ma+e\), \(a\sim N(0,I\sigma^2_a)\)

Where

• \(M\) is the genotypic matrix, \(m_{ij}=\{0,1,2\}\)
• \(K=\alpha MM'\)
• \(u=Ma\)
• \(\sigma^2_a=\alpha\sigma^2_u\)

Kernel model

\[ \left[\begin{array}{rr} X'X & Z'X \\ X'Z & Z'Z+K^{-1}(\sigma^2_e/\sigma^2_u) \end{array}\right] \left[\begin{array}{r} b \\ u \end{array}\right] =\left[\begin{array}{r} X'y \\ Z'y \end{array}\right] \]

Ridge model

\[ \left[\begin{array}{rr} X'X & M'X \\ X'M & M'M+I^{-1}(\sigma^2_e/\sigma^2_a) \end{array}\right] \left[\begin{array}{r} b \\ a \end{array}\right] =\left[\begin{array}{r} X'y \\ M'y \end{array}\right] \]

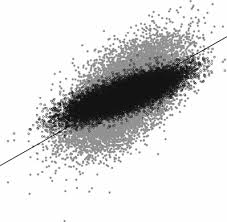
Both models capture same genetic signal (de los Campos 2015)

K = tcrossprod(M)/ncol(M)
GBLUP = reml(y=y,K=K); Kernel_GEBV = GBLUP$EBV
RRBLUP = reml(y=y,Z=M); Ridge_GEBV = M%*%RRBLUP$EBV
plot(Kernel_GEBV,Ridge_GEBV, main='Comparing results')