De-Confusion Tables

Binary Classifiers

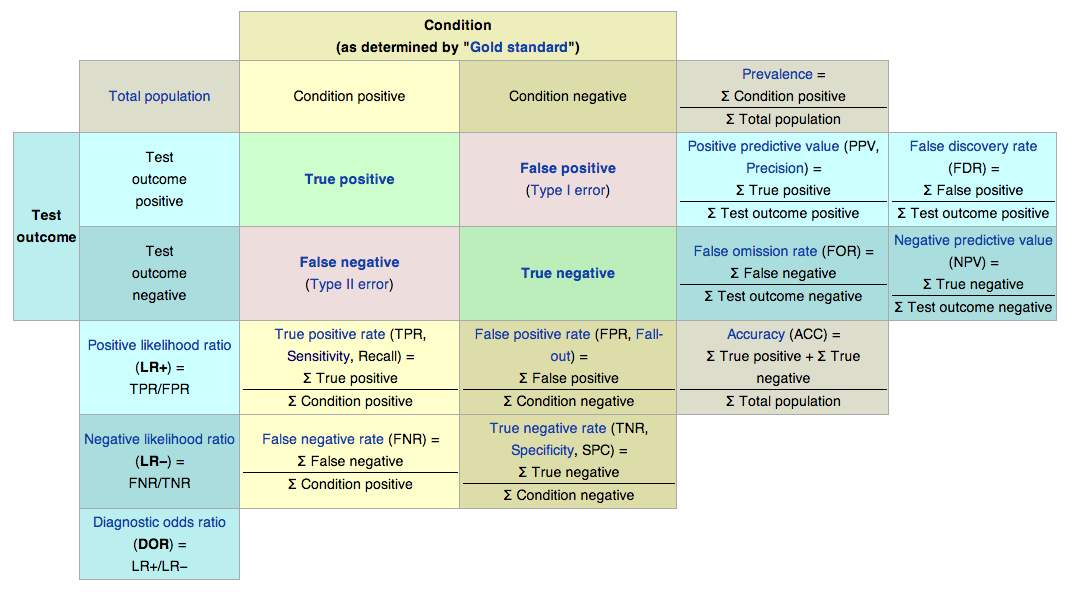
• A common task with binary classifier models is to assess its performance using a tool known a Confusion Table or Confusion Matrix
• Statistics measure different aspects of classification performance

• Source http://en.wikipedia.org/wiki/Confusion_matrix

• Type-I and Type-II errors in statistical Hypothesis testing is a special case of Binary Classification
• Type-I errors (False Positives) - Predict the alternative \(H_A\) when the Null Hypothesis \(H_0\) is true
• Type-II errors (False Negatives) - Predict the Null \(H_0\) when the Alternative Hypothesis \(H_A\) is true

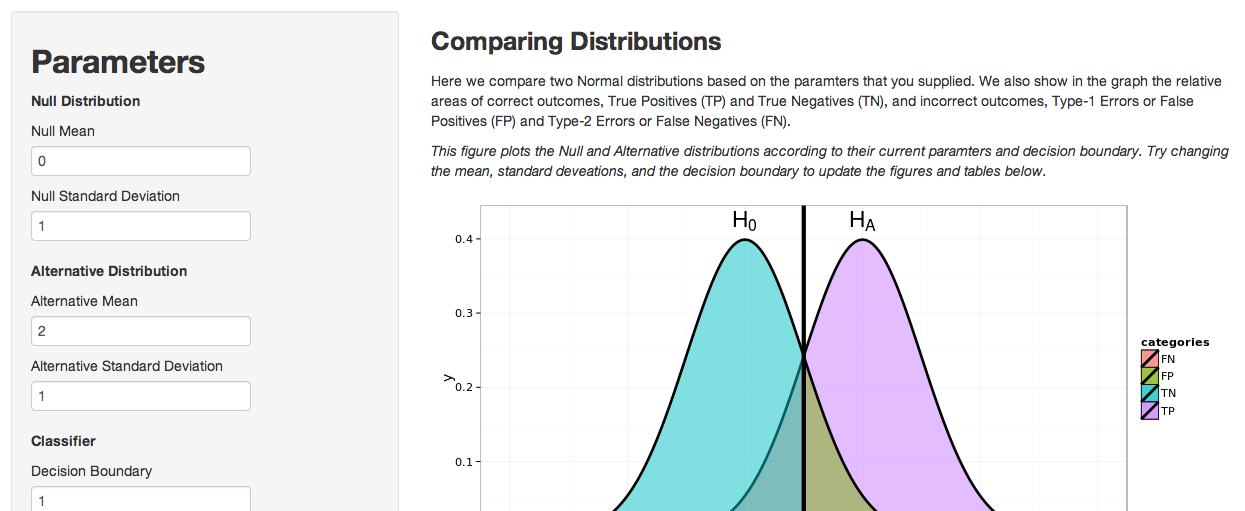
xvals <- seq(-3, 6, length = 1000)
y1 <- dnorm(xvals, mean = 0, sd = 1)
y2 <- dnorm(xvals, mean = 2, sd = 1)
df <- data.frame(x=c(xvals,xvals),
                 y=c(y1,y2), 
                 hypothesis=c(rep("H_0", length(y1)), rep("H_A", length(y2))))
lin <- 1.2 # decision boundary
library(ggplot2)

ggplot(df, aes(x,y, group=hypothesis)) +
           geom_ribbon(data=subset(df,x>lin & x<max(x) & hypothesis=="H_0"),aes(x=x, ymax=y, ymin=0, fill="False Positive")) +
           geom_ribbon(data=subset(df,x<lin & x>min(x) & hypothesis=="H_A"),aes(x=x, ymax=y, ymin=0, fill="False Negative")) +
           geom_line(size=1) +
           geom_vline(xintercept = lin, size=1.5, color="black") + theme_bw()

• De-confusion Tables is a Shiny App that allows the user modify two Gaussian densities and explore changes to confusion table statistics
• An ROC Curve can be generated to assess overall performance of the simple line-based binary classifier
• WebApp available at http://nielshanson.shinyapps.io/confusion_matrix/