20/10/2016
Correlação e regressão
Introdução
- Correlação e regressão são métodos para estimar o relacionamento entre duas variáveis numéricas
Correlação
- É uma medida da dependência entre duas variáveis
- A correlação, r, é um valor entre -1 e 1
- Quanto mais distante de 0, mais forte é a correlação
- A correlação pode ser positiva (> 0) ou negativa (< 0)
- Exemplo mais comum é a correlação linear
- Indica que a relação entre as variáveis é uma equação linear (1o grau):
- Ex.: para variáveis x e y,
y = a*x + b(onde a e b são constantes)
Força da correlação
- De acordo com seu valor, a correlação pode ser:
- -1.0 a -0.5 ou 1.0 a 0.5: Forte
- -0.5 a -0.3 ou 0.3 a 0.5: Moderada
- -0.3 a -0.1 ou 0.1 a 0.3: Fraca
- -0.1 a 0.1: Muito fraca ou nenhuma
- Essa classificação é subjetiva. Você pode encontrar outros valores em outros lugares.
Correlação linear

Correlação linear
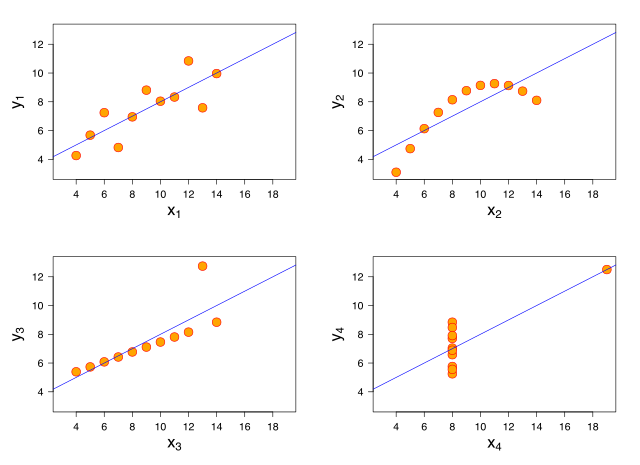
Correlação: exemplo em R
# Data set mtcars: # mpg = milhas por galão (consumo) # hp = horsepower plot(mtcars$hp, mtcars$mpg)
Correlação: exemplo em R
cor.test(mtcars$hp, mtcars$mpg) ## teste de significância
## ## Pearson's product-moment correlation ## ## data: mtcars$hp and mtcars$mpg ## t = -6.7424, df = 30, p-value = 1.788e-07 ## alternative hypothesis: true correlation is not equal to 0 ## 95 percent confidence interval: ## -0.8852686 -0.5860994 ## sample estimates: ## cor ## -0.7761684
# uma correlação pode ser alta e # não ser estatisticamente significativa!
Métodos de correlação
- Correlação linear de Pearson (paramétrico). Pressupostos: normalidade, ausência de outliers, linearidade e homocedasticidade.
- Correlação de Spearman (não-paramétrico). Mede se existe uma relação monotônica entre as variáveis (ex.: as duas crescem ou as duas diminuem).
- Correlação de Kendall (não-paramétrico). Como Spearman, porém mais adequado quando há valores iguais e amostras pequenas
- Cada método tem seus pressupostos
Correlação de Spearman

Correlação de Spearman: exemplo em R
cor.test(mtcars$hp, mtcars$mpg, method="spearman")
## Warning in cor.test.default(mtcars$hp, mtcars$mpg, method = "spearman"): ## Cannot compute exact p-value with ties
## ## Spearman's rank correlation rho ## ## data: mtcars$hp and mtcars$mpg ## S = 10337, p-value = 5.086e-12 ## alternative hypothesis: true rho is not equal to 0 ## sample estimates: ## rho ## -0.8946646
Regressão linear
- A regressão linear, além de medir a força da dependência entre duas variáveis (como a correlação), também estima os parâmetros a e b da reta que relaciona as variáveis
- É uma técnica para modelagem estatística
- Regressão linear: estimar a e b na equação linear y = ax + b de forma a obter a reta que se ajusta melhor nos dados

Regressão linear: exemplo em R
modelo <- lm(mpg ~ hp, data=mtcars) plot(mtcars$hp, mtcars$mpg) abline(modelo, col="red")
Regressão linear: exemplo em R
- O valor de
bé chamado de Intercept.
print(modelo)
## ## Call: ## lm(formula = mpg ~ hp, data = mtcars) ## ## Coefficients: ## (Intercept) hp ## 30.09886 -0.06823
Regressão linear e coeficiente de determinação
- O coeficiente de determinação, R², mede a força da relação linear entre as variáveis
- Varia de 0 (mais fraco) até 1 (mais forte)
- R² é o quadrado da correlação de Pearson entre as variáveis
Regressão linear: exemplo em R
Detalhes do modelo de regressão podem ser obtidos com summary(modelo)
Regressão linear: exemplo em R
## ## Call: ## lm(formula = mpg ~ hp, data = mtcars) ## ## Residuals: ## Min 1Q Median 3Q Max ## -5.7121 -2.1122 -0.8854 1.5819 8.2360 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 30.09886 1.63392 18.421 < 2e-16 *** ## hp -0.06823 0.01012 -6.742 1.79e-07 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 3.863 on 30 degrees of freedom ## Multiple R-squared: 0.6024, Adjusted R-squared: 0.5892 ## F-statistic: 45.46 on 1 and 30 DF, p-value: 1.788e-07
Regressão múltipla
Na regressão múltipla, consideram-se 2 ou mais variáveis independentes.
modelo <- lm(formula = mpg ~ hp + wt + cyl, data = mtcars) print(modelo)
## ## Call: ## lm(formula = mpg ~ hp + wt + cyl, data = mtcars) ## ## Coefficients: ## (Intercept) hp wt cyl ## 38.75179 -0.01804 -3.16697 -0.94162
Regressão múltipla: exemplo em R
## ## Call: ## lm(formula = mpg ~ hp + wt + cyl, data = mtcars) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.9290 -1.5598 -0.5311 1.1850 5.8986 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 38.75179 1.78686 21.687 < 2e-16 *** ## hp -0.01804 0.01188 -1.519 0.140015 ## wt -3.16697 0.74058 -4.276 0.000199 *** ## cyl -0.94162 0.55092 -1.709 0.098480 . ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 2.512 on 28 degrees of freedom ## Multiple R-squared: 0.8431, Adjusted R-squared: 0.8263 ## F-statistic: 50.17 on 3 and 28 DF, p-value: 2.184e-11
Regressão logística
- Tipo de regressão em que a variável de saída (dependente) é binária (0 ou 1)

Regressão logística
- A regressão modela os dados através de uma curva sigmoidal
- Sendo:
- x a variável independente (numérica)
- y a variável dependente (binária: 0 ou 1)
- Então o valor previsto pelo modelo de y para um determinado x é
- 0, se f(x) < 0.5
- 1, se f(x) >= 0.5
Regressão logística: exemplo em R
- Vamos tentar prever o tipo de motor de um carro a partir da sua potência
- 0 = motor em V; 1 = motor reto
| hp | vs | |
|---|---|---|
| Mazda RX4 | 110 | 0 |
| Mazda RX4 Wag | 110 | 0 |
| Datsun 710 | 93 | 1 |
| Hornet 4 Drive | 110 | 1 |
| Hornet Sportabout | 175 | 0 |
| Valiant | 105 | 1 |
| Duster 360 | 245 | 0 |
| Merc 240D | 62 | 1 |
| Merc 230 | 95 | 1 |
| Merc 280 | 123 | 1 |
| Merc 280C | 123 | 1 |
| Merc 450SE | 180 | 0 |
| Merc 450SL | 180 | 0 |
| Merc 450SLC | 180 | 0 |
| Cadillac Fleetwood | 205 | 0 |
| Lincoln Continental | 215 | 0 |
| Chrysler Imperial | 230 | 0 |
| Fiat 128 | 66 | 1 |
| Honda Civic | 52 | 1 |
| Toyota Corolla | 65 | 1 |
| Toyota Corona | 97 | 1 |
| Dodge Challenger | 150 | 0 |
| AMC Javelin | 150 | 0 |
| Camaro Z28 | 245 | 0 |
| Pontiac Firebird | 175 | 0 |
| Fiat X1-9 | 66 | 1 |
| Porsche 914-2 | 91 | 0 |
| Lotus Europa | 113 | 1 |
| Ford Pantera L | 264 | 0 |
| Ferrari Dino | 175 | 0 |
| Maserati Bora | 335 | 0 |
| Volvo 142E | 109 | 1 |
Regressão logística: exemplo em R
Regressão logística: exemplo em R
library(MLmetrics, warn.conflicts = FALSE)
# vs: tipo de motor (0 = motor em V, 1 = motor reto)
# hp: potência do motor, em cavalos
# Cria modelo de regressão logística
logreg <- glm(formula = vs ~ hp,
family = binomial(link = "logit"), data = mtcars)
# Usa o modelo para prever o tipo de motor
dados <- mtcars %>%
select(hp, vs) %>%
mutate(vsPrevisto = ifelse(logreg$fitted.values < 0.5, 0, 1))
Regressão logística: exemplo em R
Regressão logística
| hp | vs | vsPrevisto |
|---|---|---|
| 110 | 0 | 1 |
| 110 | 0 | 1 |
| 93 | 1 | 1 |
| 110 | 1 | 1 |
| 175 | 0 | 0 |
| 105 | 1 | 1 |
| 245 | 0 | 0 |
| 62 | 1 | 1 |
| 95 | 1 | 1 |
| 123 | 1 | 0 |
| 123 | 1 | 0 |
| 180 | 0 | 0 |
| 180 | 0 | 0 |
| 180 | 0 | 0 |
| 205 | 0 | 0 |
| 215 | 0 | 0 |
| 230 | 0 | 0 |
| 66 | 1 | 1 |
| 52 | 1 | 1 |
| 65 | 1 | 1 |
| 97 | 1 | 1 |
| 150 | 0 | 0 |
| 150 | 0 | 0 |
| 245 | 0 | 0 |
| 175 | 0 | 0 |
| 66 | 1 | 1 |
| 91 | 0 | 1 |
| 113 | 1 | 1 |
| 264 | 0 | 0 |
| 175 | 0 | 0 |
| 335 | 0 | 0 |
| 109 | 1 | 1 |
Regressão logística
- O modelo de regressão logística prevê o valor da variável de saída (0 ou 1)
- O valor pode estar certo ou errado
- Podemos montar uma tabela de contingência com a combinação resultado real, resultado previsto
Tabela de contingência
xtabs(~ vsPrevisto + vs, data=dados)
## vs ## vsPrevisto 0 1 ## 0 15 2 ## 1 3 12
Positivos e negativos, verdadeiros e falsos
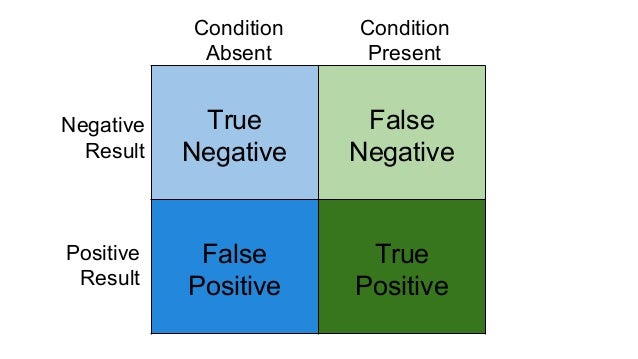
Acurácia
- Acurácia: acertos / total de registros
- = (TP + TN) / (TP + TN + FP + FN)
- = proporção de elementos na diagonal principal da tabela de contingência
Precisão e recall
Precisão e recall
F-measure ou F1 Score
- Ponderação entre precisão e recall
- F = 2 * precisão * recall / (precisão + recall)
Precisão e recall: exemplo em R
Accuracy(y_pred = dados$vsPrevisto, y_true = dados$vs)
## [1] 0.84375
Precision(y_pred = dados$vsPrevisto, y_true = dados$vs)
## [1] 0.8823529
Recall(y_pred = dados$vsPrevisto, y_true = dados$vs)
## [1] 0.8333333
F1_Score(y_pred = dados$vsPrevisto, y_true = dados$vs)
## [1] 0.8571429