Sannolikhetsmodeller och Distributioner
Rasmus Bååth
09/04/2014
Generativa modeller
- Hitils har vi kollat på modeller för medelvärden.
Generativa modeller
- Hitils har vi kollat på modeller för medelvärden.
- Om medelvärdesmodeller beskriver medelvärden så beskriver generativa modeller data.
- Några av de enklaste generativa modellerna kallas för parametriska sannolikhetsfördelningar.
- Man tänker ofta på dessa som former men de går också att karakteriseras som processer.
De grundläggande processerna
- Binomialmodellen
- Uniform-modellen
- Exponential-modellen
- Poisson-modellen
- Normalmodellen
Binomialmodellen

Binomialmodellen
- Parametrar:
- antal trials,
n - relativ frekvens,
p
- antal trials,
- Output:
- Antal successes
Binomialmodellen i R
# Generera data från modellen
rbinom(n=5, size=1, prob=0.5)
[1] 1 0 0 0 1
# Ta reda på hur sannolika olika utfall är
dbinom(x=2, size=2, prob=0.5)
[1] 0.25
Binomialmodellen i R
# Räkna ut coverage interval
qbinom(c(0.25, 0.75), size=100, prob=0.5)
[1] 47 53
# Ta reda på den kumulativa sannolikheten
pbinom(c(47, 50, 53, 100), size=100, prob=0.5)
[1] 0.3086 0.5398 0.7579 1.0000
Vad är parametriska sannolikhetsfördelningar bra till?
- Statistisk modellelering.
- Generera låtsasdata
- Powerberäkningar.
Uniform-modellen
Uniform-modellen
- Parametrar:
- min
- max
- Output:
- Ett decimaltal mellan min och max

Uniform-modellen i R
# Generera data från modellen
runif(n=4, min=-1, max=2)
[1] -0.9811 1.7193 1.5601 0.7715
# Ta reda på hur sannolika olika utfall är
dunif(x=2, min=-1, max=2)
[1] 0.3333
Uniform-modellen i R
# Räkna ut coverage interval
qunif(c(0.25, 0.75), min=-2, max=2)
[1] -1 1
# Ta reda på den kumulativa sannolikheten
punif(c(-2, -1, 0, 1, 2), min=-2, max=2)
[1] 0.00 0.25 0.50 0.75 1.00
Exponential-modellen
Exponential-modellen
- Parametrar:
- rate (1 / mean)
- Output:
- Ett decimaltal mellan 0 och \( \infty \)

Exponential-modellen i R
# Generera data från modellen
rexp(n=4, rate= 1 / 30)
[1] 53.841 26.546 11.236 1.966
histogram(rexp(n = 9999, rate= 1 / 10))
Poisson-modellen

Poisson-modellen
- Parametrar:
- mean
- Output:
- Ett heltal mellan 0 och \( \infty \)

Poisson-modellen i R
# Generera data från modellen
rpois(n=4, lambda=3)
[1] 1 3 5 1
histogram(rpois(n = 999, lambda=3))
Normalmodellen
- Oklart vad som är normalt med normalfördelningen.
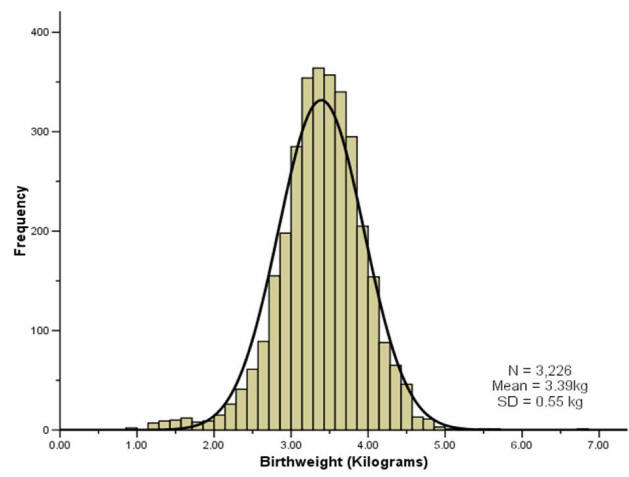
Vad leder till normalfördelningen?
- Många additiva identiskt stora slumpvisa förändringar.
- Borde längd vara normalfördelat?
Normalmodellen
- Parametrar:
- mean
- standard deviation
- Output:
- Ett heltal mellan \( -\infty \) till \( \infty \)

Normalmodellen i R
# Generera data från modellen
rnorm(n=4, mean= 10, sd=2)
[1] 8.091 10.772 9.600 7.495
histogram(rnorm(n=9999, mean= 10, sd=2))
Inget är normalfördelat
- “Är det normalfördelat?”
- Inget man behöver vara nervös för. Det är aldrig normalfördelat. Frågan är om det är tillräkligt normalfördelat.
- Med bootstrap så är detta ingen issue. Metoder som bootstrap som inte antar nån fördelning kallas ofta för icke-parametriska.
Parametriska fördelningar är toppen för att generera låtsasdata.
Låtsasdata är bra för att:
- Testa plottar och metoder.
- Få en känsla för slumpen.
- Powerberäkningar.
Exempel på datasimulering
- Du är intresserad av hur skrivprocessen beror på koncentrationsförmågan.
- Du undersöker hur många stavfel som begås för människor som skriver i tystnad och människor som skriver i brus.
I R
# För brusgruppen
rpois(n=20, lambda=4)
[1] 4 7 7 2 3 3 3 0 4 6 1 4 3 4 2 3 6 5 2 3
# För för tystnadsgruppen
rpois(n=20, lambda=3)
[1] 2 1 5 5 2 7 1 3 6 4 2 3 2 5 6 4 5 4 4 3
noise <- rpois(n=20, lambda=4)
silence <- rpois(n=20, lambda=3)
mean(noise)
[1] 3.95
mean(silence)
[1] 3
mean(noise) - mean(silence)
[1] 0.95
Använd do för att upprepa "experimentet"
do(6) * {
noise <- rpois(n=20, lambda=4)
silence <- rpois(n=20, lambda=3)
mean(noise) - mean(silence)
}
result
1 0.60
2 2.25
3 0.50
4 1.30
5 1.45
6 1.70
Ett CI för vårt "experiment"
noise <- rpois(n=20, lambda=4)
silence <- rpois(n=20, lambda=3)
s <- do(500) * {
mean(resample(noise)) -
mean(resample(silence))
}
confint(s, method="quantile")
name lower upper level method
1 result -0.75 2.05 0.95 quantile
Exempel på ännu en datasimulering
- Du är hur reaktionstiden påverkas av koffeinintag
- Du undersöker visuell reaktionstid för människor som druckit olika många koppar kaffe.
Två nya kommandon
rep(c("a", "b", "c"), each=2)
[1] "a" "a" "b" "b" "c" "c"
data.frame(y = 1:3, x=rep("a", 3))
y x
1 1 a
2 2 a
3 3 a
I R
cups = rep(0:4, each=10)
head(cups, 22)
[1] 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2
mean <- 0.3 + cups * -0.02
head(mean, 22)
[1] 0.30 0.30 0.30 0.30 0.30 0.30 0.30 0.30 0.30 0.30 0.28 0.28 0.28 0.28
[15] 0.28 0.28 0.28 0.28 0.28 0.28 0.26 0.26
d <- data.frame(cups = cups)
d$rt <- rnorm(50, mean, sd=0.1)
head(d)
cups rt
1 0 0.3372
2 0 0.3525
3 0 0.1633
4 0 0.1564
5 0 0.2147
6 0 0.4287
xyplot(rt ~ cups, data=d, type=c("p", "r"))
Jämför estimat med de riktiga värdena: intercept = 0.3 och slope coef = -0.02
lm(rt ~ cups, data=d)
Call:
lm(formula = rt ~ cups, data = d)
Coefficients:
(Intercept) cups
0.3226 -0.0296