Data Science Consultoria

Maximizando Resultados

Sergio V. Simioni

Experiência Profissional

.
.
  • Diretor Regional de Excelência Operacional - INVISTA Fibras e Polimeros
.
  • Diretor de Operações - INVISTA Fibras e Polimeros
.
  • Gerente de Site - DuPont do Brasil
.
  • Presidente do Comitê de Manufatura ( AMCHAM - biênio 2011/2012 )
.

Formação Acadêmica

.
  • Graduação: Engenharia Mecânica - Unicamp
    .
  • Pós-Graduação: Processos de Fabricação - Unicamp
    .
  • Pós-Graduação: Finanças Corporativas - FGV
    .
  • Curso Extenção: Finanças Corporativas - Ohio University
    .
  • Pós-Graduação: Economia - Unicamp
    .
  • Curso de Especialização: Big data - Johns Hopkins University by Coursera

Programas de Melhorias

Comparação
.

Teoria das Restrições

  • "Throughput" ( T ):

    > Indicador de geração de resultados através de vendas   
        ( Vendas - Custo Variável )

  • Despesas Operacionais ( DO ):

    > Custos do sistema para transformar investimento em "throughput" 
        ( Custos Fixos )

  • Investimentos ( I ):

    > Custos do sistema com materiais para obter "throughput" 
         ( Inventários )
    ( "Throughput" - Despesa Operacional ) / Investimentos

Vídeo

TOC + Lean

Proposta Data Science

line

  • ESTRATÉGIA

Identificar o mais rentável mix de produtos e implementar ações para aumentar o valor do negócio baseado no moderno conceito de análise massiva de dados, conjugando Teoria das Restrições, Lean Manufacturing, Big Data e ferramentas de modelagem matemática.

line

  • ETAPAS

Diagnóstico, Implementação e Sustentação.

line

  • OBJETIVO

Aumentar o Valor do Negócio ( EVA )

Valor do Negócio

.

EVA ( Valor Econômico Adicionado )

ROIC (Retorno s/ Capital) vs. Competição

.

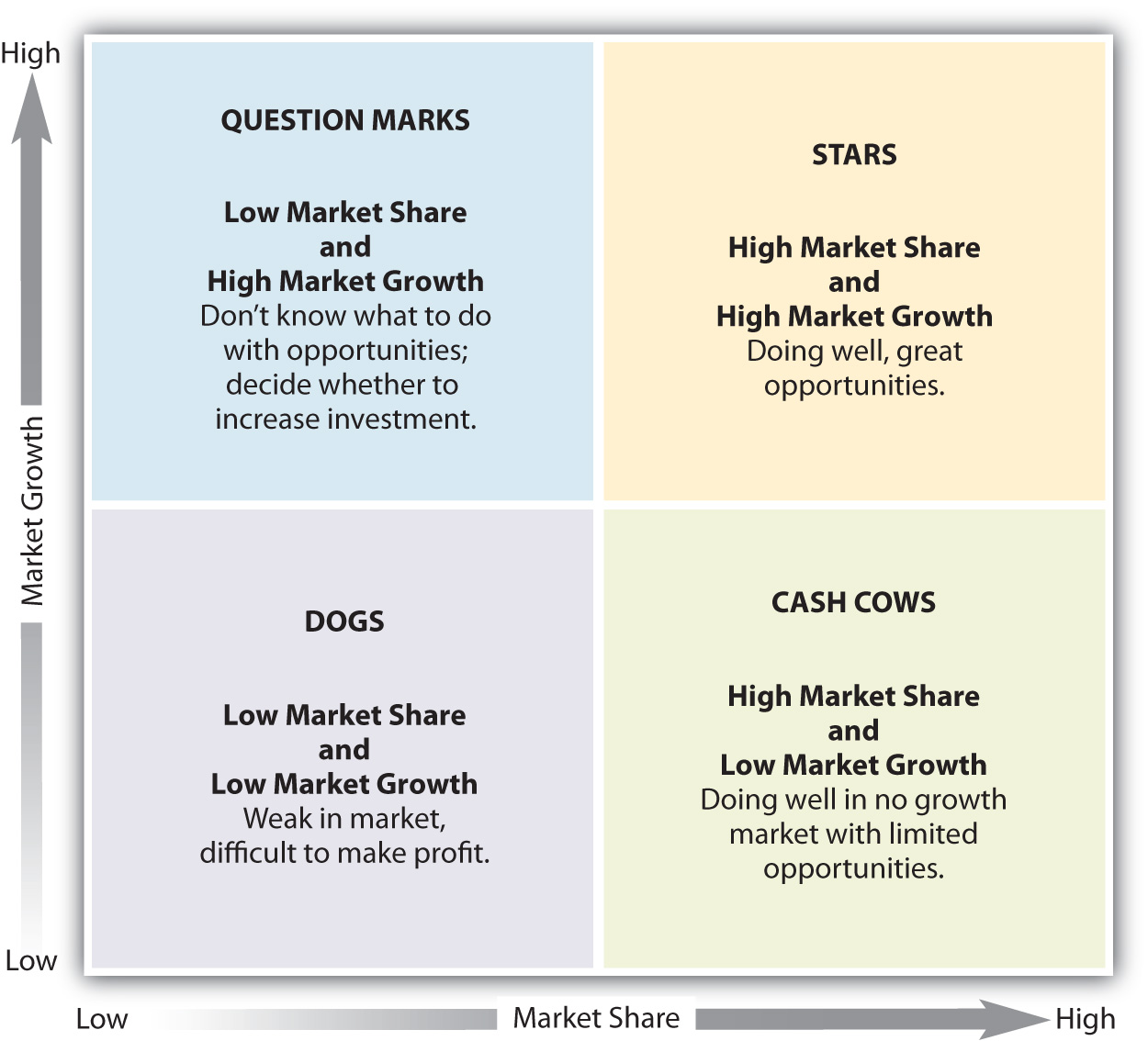
Matriz CrescimentoXShare BCG

.
Otimizando o Mix de Produtos

ETAPA DIAGNÓSTICO

Tópicos Avaliados na Etapa Diagnóstico

.
.
  • Ranking dos Produtos mais Rentáveis
.
  • Modelagem do Mix Ótimo de Produtos
.
  • Identificação dos Gargalos ( TOC )
.
  • Quantificação do Potencial de Elevação do EVA

Exemplo Hipotético

Modelagem do Mix de Produtos

Com uso de Programação R

library(lpSolveAPI)
library(ggplot2)
library(knitr)
model<- make.lp(0,4)
name.lp(model, "Production Best Mix")
set.objfn(model, c(26,35,25,37))
set.bounds( model, lower = c(1,1,1,1), upper = c(Inf,Inf,Inf,Inf))
set.type(model, c(1,2,3,4), type=c("real"))
coef1<- c(1.7,2.1,1.4,2.4)
add.constraint(model, coef1, "<=", 28)
coef2<- c(1.1,2.5,1.7,2.6)
add.constraint(model, coef2, "<=", 35)
coef3<- c(1.6,1.3,1.6,0.8)
add.constraint(model, coef3, "<=", 21)

print(model)
## Model name: Production Best Mix
##             C1    C2    C3    C4        
## Maximize    26    35    25    37        
## R1         1.7   2.1   1.4   2.4  <=  28
## R2         1.1   2.5   1.7   2.6  <=  35
## R3         1.6   1.3   1.6   0.8  <=  21
## Kind       Std   Std   Std   Std        
## Type      Real  Real  Real  Real        
## Upper      Inf   Inf   Inf   Inf        
## Lower        1     1     1     1

Solução otimizada

get.objective(model)
## [1] 469.9805
get.constraints(model)
## [1] 28.00000 32.32532 21.00000
get.variables(model)
## [1] 1.000000 7.922078 5.188312 1.000000

Conclusão

.

O problema foi analisado utilizando-se o pacote de programação lpSolveAPI, sendo que a equação que maximiza a rentabilidade sem violar nenhuma das restrições impostas é:

.

Volume Produto 1 = 1.00 ton
Volume produto 2 = 7.92 ton
Volume Produto 3 = 5.19 ton
Volume Produto 4 = 1.00 ton

.

26 x 1.00 + 35 x 7.92 + 25 x 5.19 + 37 x 1.00

.
Ganho maximizado = U$ 469,98M

PRODUTOS DA ETAPA DIAGNÓSTICO

Dados Necessários

  • Demonstrativo de Resultados mensal dos últimos 5 anos
.
  • Preço de Venda e Volume mensal de cada produto dos últimos 5 anos
.
  • OEE ( Overall Equipment Effectiveness) ou equivalente mensal dos últimos 5 anos
.
  • Detalhamento do OEE mensal com as principais causas 80X20 que impactaram a performance da area identificada como restrição
.
  • Custos variáveis de cada produto ( Materia Prima, Enegia e Mão de obra )
.
  • Capacidade das maquinas e processos bem como velocidade de produção dos produtos vinculados a restrição

Produtos a serem entregues

.
  • Matriz de Crescimento X Share ( BCG )
.
  • Análise de contribuição marginal de cada produto
.
  • Mix de produtos otimizado
.
  • Identificação da restrição "gargalo" com suas principais causas
.
  • Plano de implementação sumarizado para eliminação da restrição
.
  • Potencial de elevação do EVA
.